Intro to Genetic Programming: Can Evolution Write Computer Programs?

Evolution is a powerful force. It has generated the incredible diversity of life around us — from viruses to the human brain, and even tapirs. But can it also write computer programs?

Genetic Algorithms

I’m sure you have heard about the genetic algorithm. It is a method of solving optimization problems that is based on natural selection, the process that drives biological evolution.

One classic (and somewhat artificial) problem that the genetic algorithm can solve is the backpack problem.

It goes like this: You have a backpack and a set of items. Each item has a weight and a value. You need to pack the items into the backpack so that the total weight does not exceed its maximum capacity, while simultaneously maximizing the total value of the items.

Let’s say you have a backpack that can hold 5 kg and the following items:

Item Weight Value
Laptop 3 kg 150 €
Book 2 kg 100 €
Phone 1 kg 50 €
Watch 1 kg 70 €

A combination of items is called a solution or, in the context of the genetic algorithms, an individual. The solution can be represented as a binary string (a string that consists of 0s and 1s). For example, the string 1010 means that you put the laptop and the phone into the backpack. A set of solutions (individuals) is called a “population”.

The genetic algorithm works as follows:

  • Step 1. Randomly generates the initial population. In our case, the population could consist of the following individuals:

    Individual
    1000 (take only the laptop)
    0110 (take the book and the phone)
    1110 (take the laptop, the book and the phone)

  • Step 2. Evaluates the fitness of each individual in the population. In our example, the fitness is the total value of the items in the backpack. Note that the fitness of the last individual is 0. This is because its total weight exceeds our constraint (the maximum capacity of our backpack).

    Individual Total Weight Total Value
    1000 3 kg 150 €
    0110 3 kg 150 €
    1110 6 kg 0 €

  • Step 3. Selects the best individuals (“parents”) from the population. The selection is based on the fitness of the individuals. The higher the fitness, the higher the chance to become a parent. In our example 1000 and 0110 will become the parents.

  • Step 4. Creates a new population by either crossing over or mutating the parents. The crossover is a process of creating a new individual by combining two parents. The combining can be done in different ways. For example, you can take the first half of the first parent and the second half of the second parent.
    The mutation is a process of changing an individual randomly. In our example the new population could be: 1010, 0100, 1001, where the first two individuals are the result of the crossover and the last one is the result of the mutation of one of the parents.

  • Step 5. Goes to Step 2.

The algorithm ends when, on Step 2, the fitness of the best individual is higher than some predefined threshold or the maximum number of iterations (also called “generations”) is reached.

In our example, the algorithm will likely find the best individual after just a few iterations. It is the individual 1011 that represents the combination of the laptop, phone and watch with a total value of 270 €. However, just like in the real evolutionary process, the algorithm does not guarantee the outcome of finding the most fit individual.

From Genetic Algorithms to Genetic Programming

Let us now replace the backpack items with the instructions of a programming language. Now, our individuals become computer programs. The fitness of the individuals is evaluated based on the result of the program execution. The crossover and mutation stay almost the same (we will return to them below).

Using genetic algorithms to create computer programs is called genetic programming.

Finding the Right Language

So, what programming language should we use to represent the individuals, i.e., our computer programs? Not every language suits this task.

Consider, for example, the next valid C# code:

1
2
int i = 10;
int j = i - 2;

Now, imagine that due to the crossover or mutation, the instructions have swapped:

1
2
int j = i - 2;
int i = 10;

This program will not compile. In fact, almost all the individuals produced by crossover and mutation will be invalid programs, meaning that we won’t even be able to calculate their fitness. Clearly, C# and similar languages are too strict for genetic programming. We need a more forgiving language.

One obvious option is Perl: it is so forgiving that 93% of paint splatters are valid Perl programs.

The other option is Push. It is also very forgiving, however, it has an additional advantage: since it was created specifically for evolutionary computation, there is a significant number of genetic programming libraries for Push.

Push

Push is a very simple stack-backed interpreted language. The interpreter reads the instructions from left to right. If it sees a number, it pushes it to the stack. If it sees an operation, it pops the necessary elements from the stack, applies the operation to them and pushes the result back to the stack.

In addition to the integers, Push has a few more types of data: boolean, float, code, exec and name, each of which has its own stack. You can read more about Push in the official description.

Whatever remains on the stack after the final instruction is considered the result of the program’s execution.

Our C# example would look like this in Push:

1
(10 2 integer.-)

It instructs the Push interpreter to:

  1. Push 10 to the integer stack.
  2. Push 2 to the integer stack.
  3. Pop the top two numbers from the integer stack, subtract the second number from the first, and push the result back onto the stack.

The result of the program execution is 8.

The second example would be:

1
(2 integer.- 10)

It says to the interpreter:

  1. Push 2 to the integer stack.
  2. Pop the top two numbers from the integer stack, subtract the second number from the first, and push the result back onto the stack. If there are not enough numbers on the stack, ignore the instruction and proceed as if nothing happened.
  3. Push 10 to the integer stack.

The result of the program execution is two numbers: 10 2.

Psh: Genetic Programming with Push

After checking the available Push implementations, I ended up using Psh — a Push interpreter and genetic algorithm written in Java. It supports most of the Push instructions and the main stages of genetic algorithms (including crossover and mutation).

The Problem: Checking if a Number is Even

Let’s consider a simple problem: checking if an integer number is even.

I bet you would solve it like this:

1
bool IsEven(int number) => number % 2 == 0;

Or maybe like this:

1
bool IsEven(int number) => (number & 1) == 0;

And this is the Push solution, assuming the input is already on the top of the integer stack:

1
(2 integer.% 0 integer.=)

Setting Up Psh

Now, let’s see how the evolutionary process tackles this task by setting up the genetic programming problem in Psh.

We will run the genetic algorithm for up to 10000 generations, maintaining a population of 700 individuals. In each generation, 70% of the population will be selected for crossover, and 30% will undergo mutation.

Our fitness function evaluates a Push program by running it through 50 tests.

Each test uses a randomly chosen integer from the range [-1000000000, 1000000000] as input. The Push program processes this integer, then the fitness function retrieves the top value from the program’s boolean stack as its output. This output is then checked against whether the input integer is actually even or odd.

If the program’s output correctly matches the parity (even or odd) of the input, the test contributes 0 to the total error. If the output is incorrect, the test contributes 1000 to the total error.

After all 50 tests are completed, the fitness function calculates and returns the average error across all tests.

How to Perform Crossover on Push Programs

Remember that crossover is the process of creating a new individual by combining its parents.

So, how do we combine two Push programs?

A program is a tree of instructions, and Push programs are no exception. To combine two trees, we can select a random node from each tree and swap the subtrees that root from that node. The result is two new trees. Since we only need one new individual, we can discard one of the new trees.

For example, if we have the next two trees and the random nodes are marked with yellow:

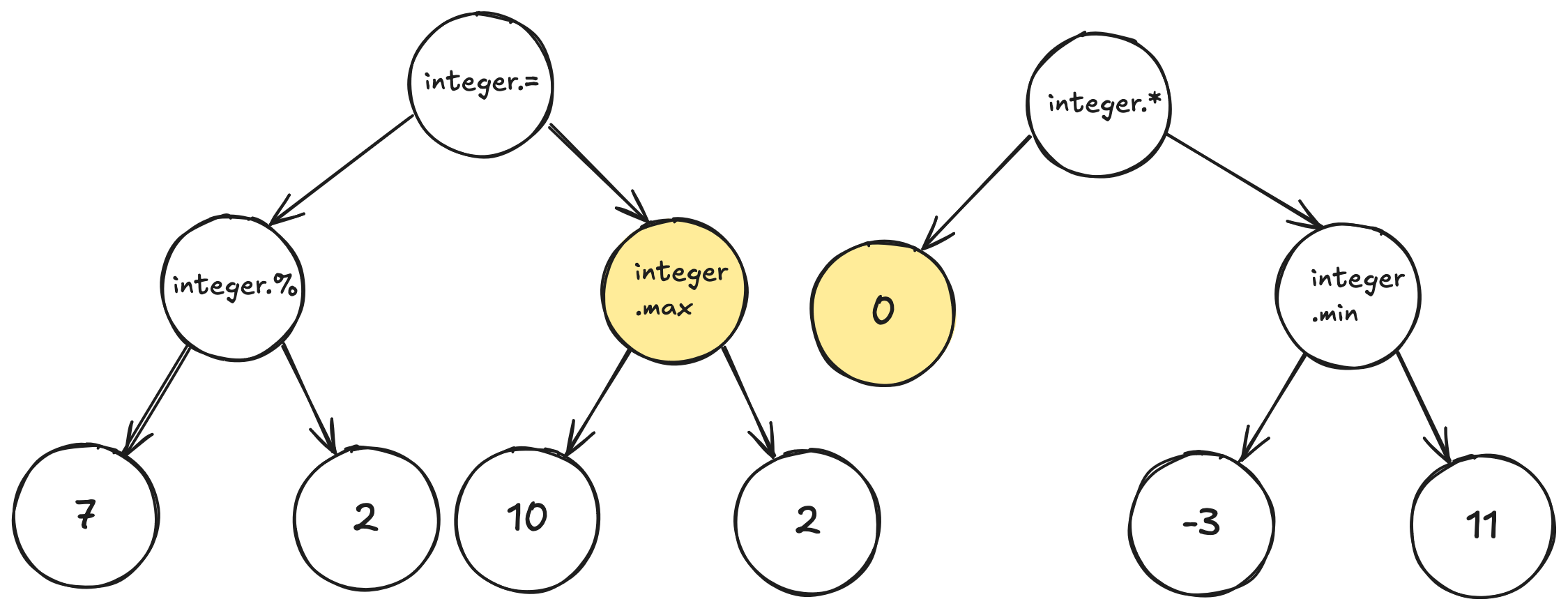
Then the result of the swapping is:

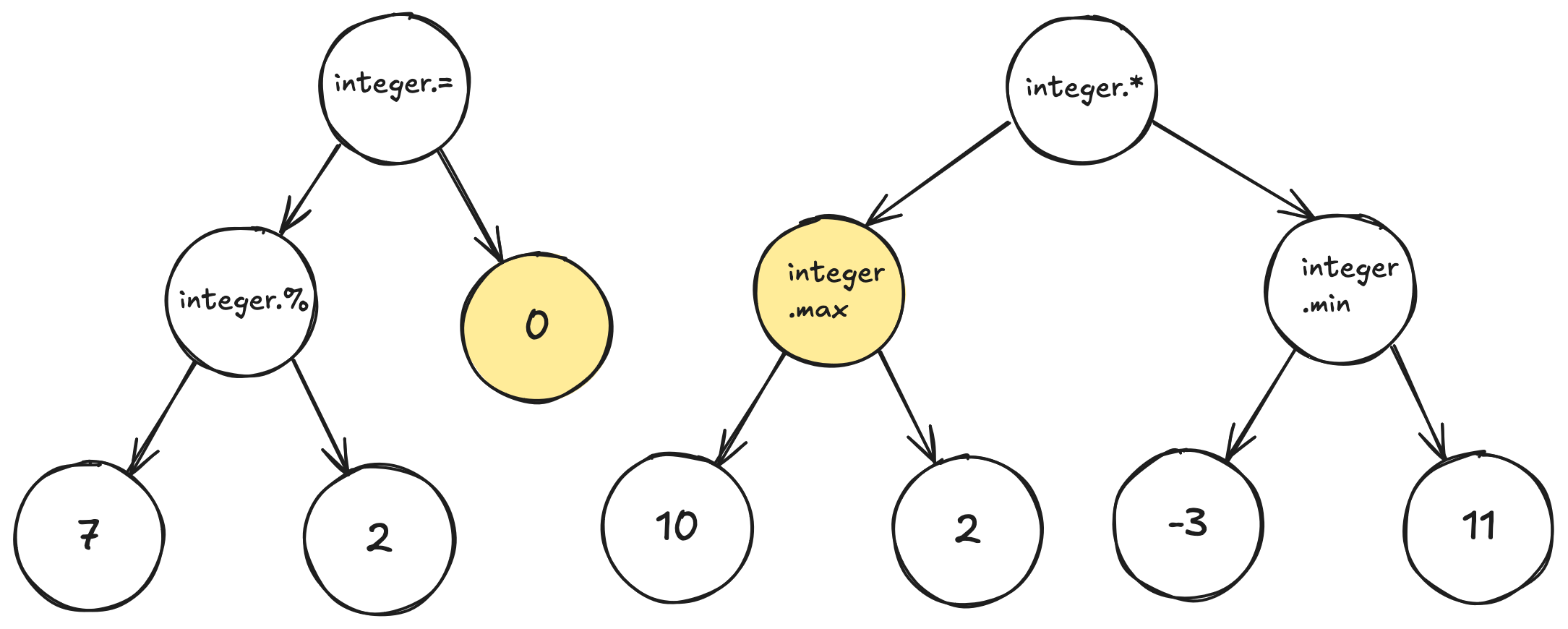
Now we can discard one of the trees and use another one as the new individual.

How to Mutate a Push Program

To mutate a Push program, we must select a random subtree and replace it with another randomly generated tree of instructions.

For example, the subtree that grows from the node marked with red:

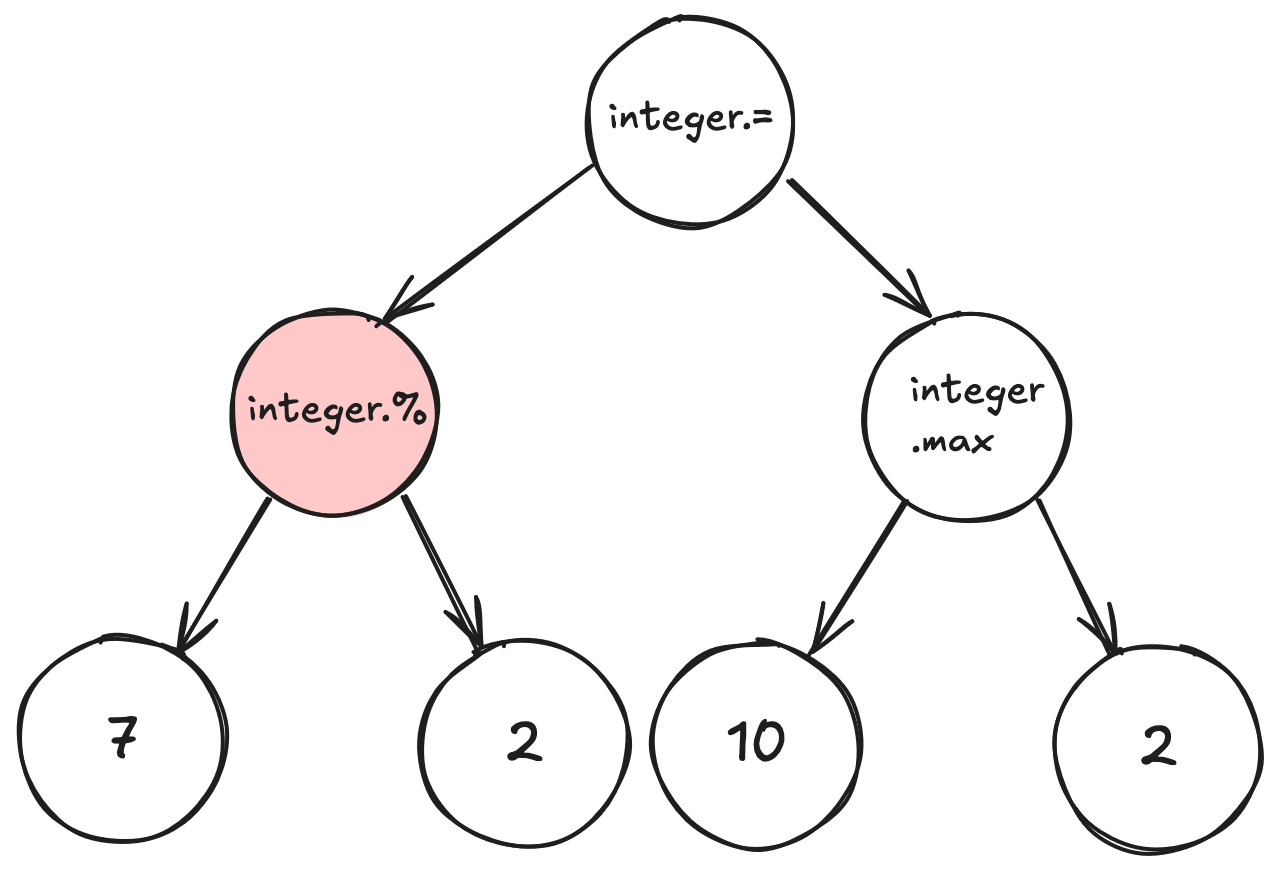
May mutate into another subtree:

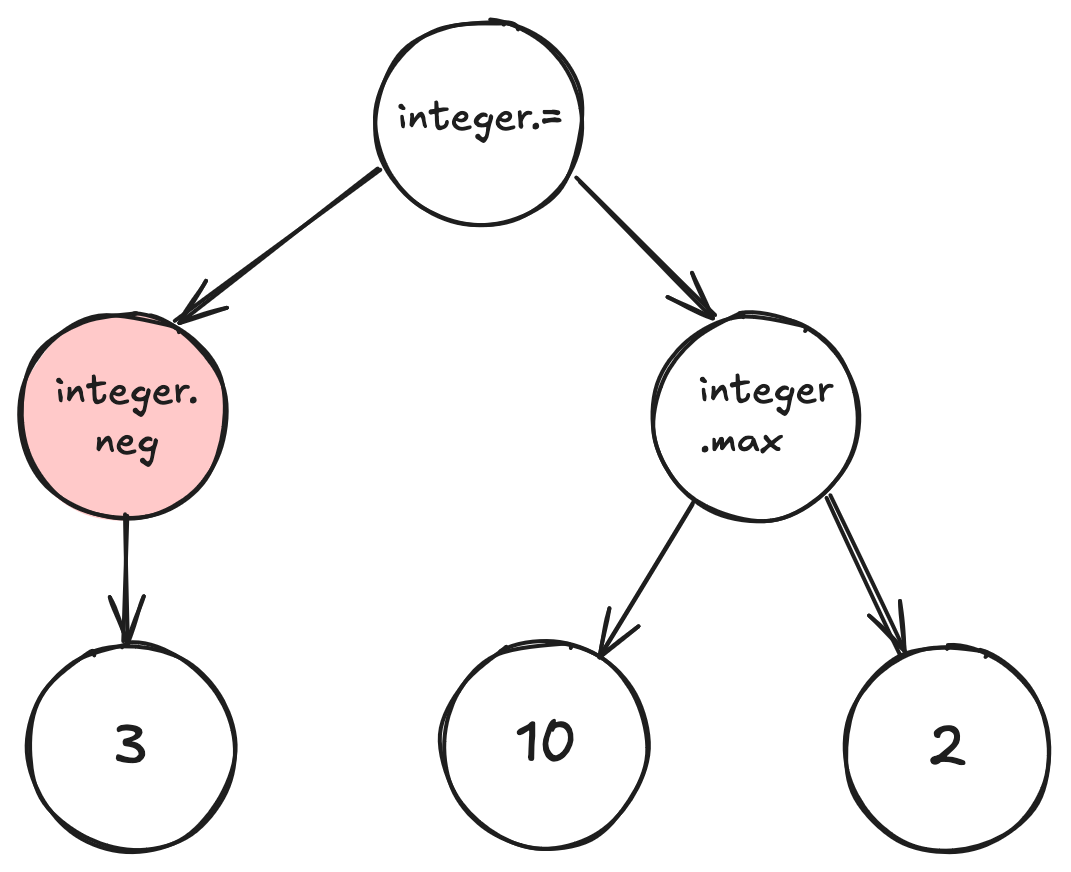
Running Psh

We are finally ready to run the genetic programming and see what evolution comes up with.

I ran it multiple times. In each run it found a solution within 200 generations. The solution consistently produced correct answers for all the tests that the fitness function executed.

For each generation, Psh printed output similar to this:

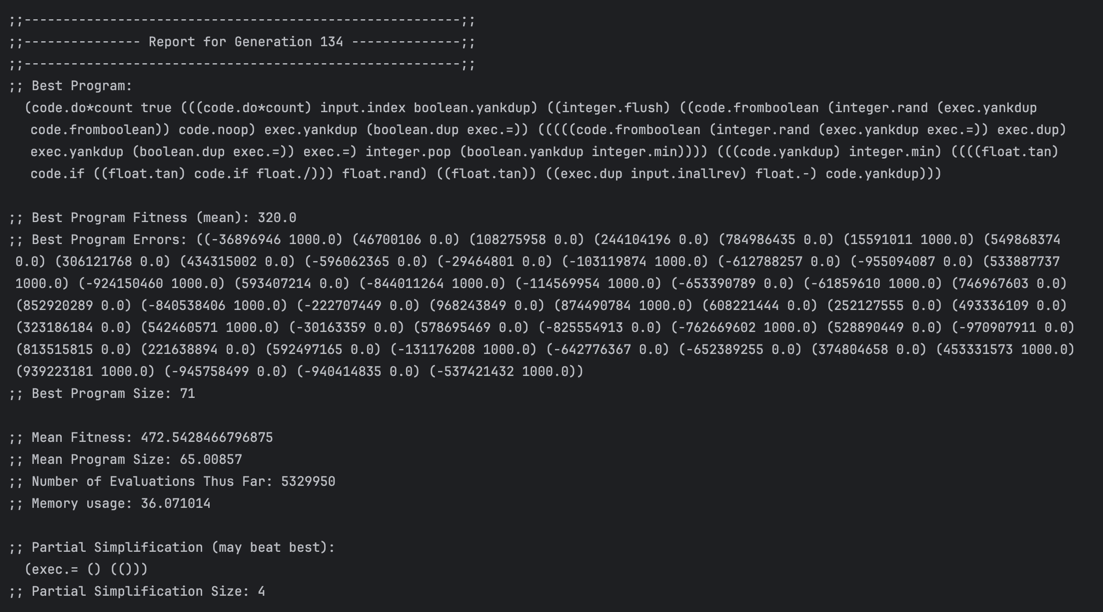
The final output included the best individual found by the genetic programming. Let’s take a look at a few of them.

Solution 1: Almost Perfect

Let’s start from the neatest solution that evolution has found:

1
2
(exec.stackdepth 
    (integer.% boolean.frominteger boolean.not) float.dup)

It is equivalent to the following C# code:

1
bool IsEven(int number) => !Convert.ToBoolean(number % 2);

Note how it invented the number 2: it’s just the depth of the execution stack at the beginning of the execution (exec.stackdepth).

The solution is also performing dummy work that does not bring us any closer to solving the problem (float.dup). This is a consequence of the fitness function imperfection. Indeed, our fitness function is not picking the most concise and efficient solutions. Just like in the real world: if natural selection does not endorse a trait, the next generations will most likely not have it.

Solution 2: Less Expected

Here’s another way to check if a number is even. It involves more elaborate Push instructions:

1
(false code.quote boolean.not code.stackdepth code.do*range)

code.do*range executes an instruction that is on the top of the code stack |p - q| + 1 times, where p and q are the top two number on the integer stack.

In our case, the top two numbers on the integer stack happen to be 2 and our input number n, the instruction is boolean.not and the value on top of the boolean stack is false. So the program, essentially, applies boolean.not to false n - 1 times.

If n is even, then n - 1 is odd, then the result is true. If n is odd, then n - 1 is even, then the result is false.

An equivalent C# code would be:

1
2
3
4
5
6
7
8
9
10
11
bool IsEven(int number)
{
    var increase = 2 <= number;
    var answer = false;
    for (var i = 2; increase && i <= number || !increase && i >= number; i = increase ? i + 1 : i - 1)
    {
        answer = !answer;
    }

    return answer;
}

It also illustrates how code.do*range works: it runs given instructions in a loop, adjusting the current index—either increasing or decreasing it—to move closer to the destination index.

Solution 3: The Most Unconventional, Yet Functional

This is probably the most inefficient way to check if a number is even, so I wouldn’t recommend using it in production. However, it’s fascinating to see how evolution arrived at this solution in such an unexpected way. It perfectly illustrates that evolution can be highly inventive, but it doesn’t aim to find the best possible solution — only one that is good enough for survival, which, in the case of genetic algorithms, is formalized as a fitness function.

1
2
3
4
5
6
7
8
9
10
11
12
(
    integer.abs
    integer.negtrue
    integer.dup
    integer.abs
    integer.pow
    exec.do*times
    code.=
    exec.=
    code.dup
    exec.do*times
)

It is equivalent to the following C# code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
bool IsEven(int number)
{
    const int executionLimit = 150;
    var answer = true;
    var numberOfIterations =
        Math.Pow(-Math.Abs(number), Math.Abs(number));
    for (var i = 0; i < numberOfIterations; i++)
    {
        if (i == executionLimit)
        {
            return answer;
        }

        i = i + 1 - 1; // Do some dummy work
    }

    answer = false;

    return answer;
}

If number is odd, Math.Pow(-Math.Abs(number), Math.Abs(number)) evaluates to a negative value, and the program immediately returns false.

If number is even, Math.Pow(-Math.Abs(number), Math.Abs(number)) is positive, so the program proceeds into the loop, where the most interesting behavior occurs.

Inside the loop, the program exploits the fact that an execution-limit of 150 instructions was imposed during evolution. This limit means that no program (individual) could execute more than 150 instructions during fitness evaluation. Crucially, for nearly all integers, Math.Pow(-Math.Abs(number), Math.Abs(number)) is greater than 150. As a result, the program never reaches the answer = false line. Instead, it exits the loop and returns true.

However, for the numbers -2, 0, and 2, Math.Pow(-Math.Abs(number), Math.Abs(number)) is less than 150. In these cases, the program produces incorrect results.

This behavior further illustrates a key characteristic of genetic programming: it produces solutions that excel at meeting the fitness function’s specific requirements, even if they are not optimal or entirely correct. As mentioned earlier, the fitness function in this scenario does not prioritize conciseness or efficiency. Additionally, it does not fully account for edge cases like numbers near zero. Similarly, the execution-limit acts as an implicit constraint within the fitness function, and the evolutionary process has exploited this limitation to achieve success within the given parameters.

To Summarize

Can evolution write computer programs? Sure, it can. And it can be very creative. But as programmers, we must pay close attention to how we set up the evolutionary process. In particular, we need to design the fitness function carefully.

The true power of genetic programming lies in its ability to find solutions for tasks that are difficult for humans to solve. Next time, we’ll take a look at one such task. Stay tuned!

Categories: genetic-algorithm, genetic-programming, push, psh
dark
sans